|
"Would you like a banana?"
"I'd like half a banana." "You'd like to halve a banana." "Yes, I'd like to have half a banana. Could you halve the banana for me?" "I'll halve the banana so you can have half the banana. ... You had that half banana pretty fast." "Yes, I have had a halved banana." "Have you enjoyed your halved banana?" "I have enjoyed it. I might enjoy the other half." "You have had a halved banana. You could have the other half if you'd like." "I would like to have more banana. Could you halve it for me?" "I have halved the half banana. Have it." "Thank you for halving the halved banana for me." "You must like that banana. You now have had a halved half banana." "The banana is quite delicious. Would you like to have the halved half remaining banana?" "I'll halve it so we both can have it." "You have had a halved halved half banana." "And you have had a half banana, and a halved half banana, and a halved halved half banana. Have you enjoyed it?" "I have."
0 Comments
I recently wrote some code for a random vector accumulator. It worked pretty fast. But the reason it worked fast was because it was just a matrix multiplication between a word-by-word matrix and a matrix of random vectors. Upon reflection, I came to the frustrating conclusion: A random vector accumulator doesn't do anything that a word-by-word co-occurrence matrix doesn't do. Specifically: if the random vectors are defined as having a length of one, and a cosine similarity of zero with any other vector, then a sparse vector where only one element is one and the rest of the elements are zero fulfills this requirement. In this way, a count matrix can be construed as a special case of the random vector accumulator. Additionally, the random vectors add no information in addition to a word-by-word count matrix. Below are two MDS renderings of a given word list. First is the rendering for the RVA, the second is the rendering for the WxW matrix. The bidimensional regression yields an r value of 0.996, quantitatively demonstrating that the two renderings are a near-perfect match (only near-perfect because of the small amount of noise from the random vectors). 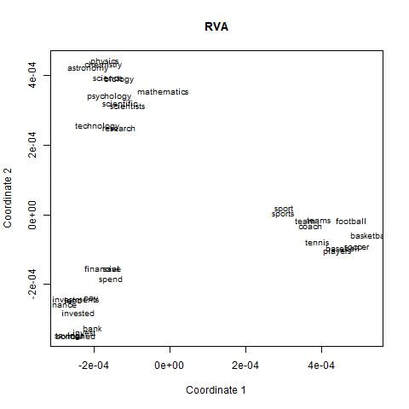 MDS projection of a selection of words (used in Jones & Mewhort, 2007). The words are drawn from three clusters in order to demonstrate the model's ability to correctly group similar words. The random vectors have 1000 elements/dimensions. 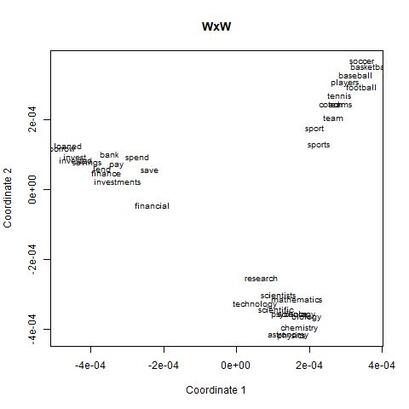 The word by word matrix is a raw frequency count of words that co-occur in the same context. Context is arbitrarily defined - here it's the co-occurrence of words within a paragraph. Upon further reflection (after it was pointed out to me), I realized that the nearly perfect reproduction of the WxW matrix by the RVA is a feature rather than a bug. While the RVA doesn't serve to reveal any latent relationships between words, it effectively compresses the matrices. The WxW matrix is ~95,000x95,000. The RVA matrix is ~95,000x1000, effectively (and with high accuracy) reducing the matrix to one one-hundredth of the size. (In practice, I used a scipy.sparse.csr_matrix to implement the count matrix - storing a 95,000x95,000 matrix in my computer's memory would be a mission; additionally, the transformation from a WxW matrix to an RVA is a simple matrix multiply between two matrices. The computation is sped up if I only use the words of interest from the WxW document. In this example, it was a matrix multiplication of my W'xW matrix [35,95000] and my random vectors [95000,1000] - which is a pretty quick computation. I've posted the code here.) In order to satiate my interest in RVAs, I looked at the ability of an RVA to reproduce the distributions of a random set of 1000 words at varying dimensionalities. 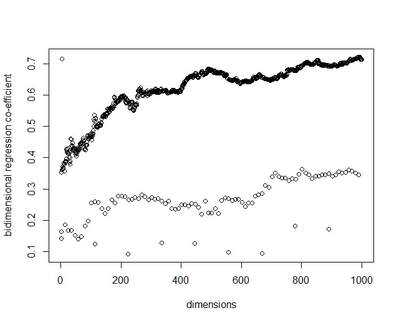 The x-axis is the varying number of dimensions. The y-axis is the bidimensional regression co-efficient (Friedman & Kohler, 2003; bidimensional regression is a measure of how well two plots match each other, independent of flips or rotations) Note that the RVA performance peaks at 0.7 rather than 1 (as in the above example). This is due to an interaction of the word set and the bidimensional regression measure. Plots that are well-clustered are generally easier to reproduce. Since I chose random points, any reproduction of the plot is going to be much noisier (I don't have a mathematical explanation for this, it's based on intuition earned from another project regarding spatial layouts; potentially forthcoming as a blog post).
There are a couple interesting points to note about this plot. First, there is a roughly linear increase in performance with dimensionality. This is to be expected. But there's this weird harmonic looking thing happening, where at certain intervals, the model drops in performance. I don't have any explanation for this (but I ran it multiple times to the same effect). It's neat, but weird. In final consideration, using a sparse matrix may still be more efficient. With a sparse matrix, I may have to store fewer actual elements than if I store a random vector. Potentially, instead of a random vector, there could be optimal vectors that I could use to reduce dimensionality while also reducing the actual number of elements that have to be stored. |
AuthorIt's bad right now. It'll get better. Archives
March 2021
Categories
All
|
 RSS Feed
RSS Feed
