|
A common theme my advisor brings up is the idea that cosine similarity is not what humans do. I want to break that down a bit and consider what that means with regard to the representation of modalities in semantic vectors. The typical way to make use of text-derived semantic vectors is to evaluate the similarity between words (aka the cosine similarity) and compare the similarities produced by the model against similarities produced by human judgments. With this approach, the extent of the usefulness of semantic vectors is something like a k-nearest-neighbors application. Of course, knn is useful for categorization. However, knn can't be the entirety of the usefulness of semantic vectors (an ideological stance that I will pursue until I find evidence ... like a good scientist). Instead of the extent of the usefulness of semantic vectors being in knn, we can treat the distribution of points in high dimensional space as meaningful and useful as is. And just as with (nonmetric) multidimensional scaling, which is rotation and scale invariant (among other things), the exact location of a word in high dimensional semantic space isn't inherently meaningful. It's the position of a word relative to another word. Likewise, MDS is often applied such that the dimensions become interpretable in some way. In a high dimensional semantic space, the dimensions likewise aren't inherently meaningful, but it seems likely that I ought to be able to rotate the semantic space in order to yield meaningful dimensions. 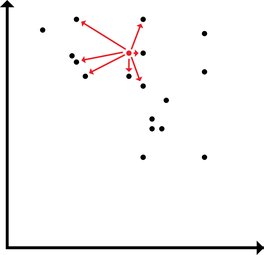 Typically, the usefulness of a vector in semantic space is applied by comparing discrete positions of a given word to the positions of other surrounding words (or of words that we would expect a model to produce a given similarity rating for). 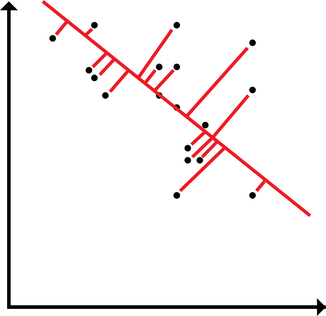 However, words may be distributed in space along some arbitrary high dimension latent within the structure that maximizes the relationship between a word in high dimensional space and some external behavior. Here, I demonstrate how words could load onto a latent dimension, where the latent dimension could predict, say, modality ratings yielded by participants. The way a word may load onto a particular modality may be latent and unobservable directly in the nearness between words in the semantic space, but may be retrievable. A simple way to implement this would be linear regression. Using sensorimotor norms as a target to predict, we could draw a line through the high dimensional space and see how each word loads onto the line. Alternatively, we could render interpretable dimensions by constructing a rotation and shift matrix. By rotating and shifting the matrix, a given dimension could be used to predict something like sensorimotor norms. Additionally, the space could be rotated to maximize each of the modalities in the norms (and then, following from the GCM, decisions could be made by applying different attentional weights to a different dimensions depending on the task. I tend to like the second approach better, but regression is easier to implement off the top of my head. Stay tuned to see whether I actually try this out! :D Note to self: I could do something like multi-fold testing in data mining using a rotation matrix yielded by procrustes analysis. I could build the rotation matrix using some subset of the data, then test the rotation matrix using the other partition. I rather prefer this to linear regression (I suppose, it's a multi-constraint linear regression): it preserves the space, and it can be interpreted in terms of a neural network.
0 Comments
This is a continuation of an earlier analysis. In summary, I used an artificial grammar to demonstrate that the cosine similarities predicted by a variety of DSMs could be well-characterized as linear combinations of direct measures of first and second order information. I just had the idea that I could potentially use the linear model trained on the artificial grammar to predict similarities in natural language corpora. Using the same artificial grammar, I measured the first and second order information in the corpus (specifically, I used the jaccard index to measure the first order information, and a modification of the jaccard index to measure second order information; I should probably post about those measures sometime). I then trained a cbow model on the artificial corpus, and generated a cosine similarity matrix. I then trained a linear using scikit-learn to predict the cbow similarities using the measures of first and second order information. THEN I trained a cbow model on a natural language corpora. A small and easy one I have on hand is the tasa corpus (preprocessed, removing stop words, punctuation, but no lemmatization). I sampled a subset of 50 words randomly, and generated a cosine similarity matrix (I didn't do the entire corpus - there are 65,000 words - my computer can't handle a 65,000x65,000 matrix). I also measured the first and second order information for those same words in the TASA corpus. FINALLY I predicted the cbow similarities for the tasa corpus using the first and second order measures for the tasa corpus. AND!! It didn't work. The r^2 for the predicted data was well into the negatives. as it turns out, a linear model trained on a small amount of data doesn't extend well to naturalistic data. Who knew? 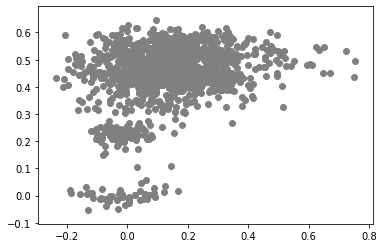 This boring looking plot is a scatter plot of the expected values against the predicted values. Along the x-axis are the cbow cosine similarities (expected), and the y-axis are the linear model predictions. While the plot looks promising, we don't get a significant prediction of the data. Wouldn't it be nice if we lived in a world where my simple prediction had been accurate? As it is, the regression produced by predicting cbow similarities in the artificial grammar do not generalize to predict the cbow similarities in the natural language corpus. Does this nullify my earlier claim that DSMs can be well-characterized as a linear combination of first and second order information? We'll see... I performed the same analysis as in the demonstration using the artificial corpus. I generated a linear model predicting cbow cosine similarities using measures of first and second order information. Instead of performing the regressions in R or using scikit-learn, I used the statsmodels api (statsmodels gives me significance values, where I'd have to calculate them with scikit).
Linear Model - Artificial grammar: cbow_sim = constant + first_order*b_0 + second_order*b_1 b_0 = -1.4*** b_1 = 1.06*** (magnitude and direction of coefficients indicates that cbow_sims are well-characterized by second order information) r^2 = 0.78 Linear Model - Natural Language Corpus: cbow_sim = constant + first_order*b_0 + second_order*b_1 b_0 = 0.19 b_1 = 0.41*** (only coefficient for second order information is significant; not large, but still significant whereas the coefficient for first order information doesn't contribute significantly to the model) r^2 = 0.11 The amount of variance predicted by the linear models significantly drops when I try to characterize cbow similarities in terms of first and second order information. First, I should note that the models DO still support my claim regarding first and second order information. The drop in the variance predicted by the linear models may be due to multiple things. First, the measure of first and second order information might not be well suited for statements longer than three words (as three word statements are used in the artificial grammar). Second, I may not be training the cbow model adequately (or, the parameters of the cbow model aren't lined up to match the assumptions of the measures of first and second order information. ... I'm going to rerun something). Is it likely that cbow is doing something qualitatively different in the natural language corpus from the artificial grammar? probably not. While I haven't put in the effort to test whether a linear model recreates the prediction of first vs second order information for every DSM I tested in my earlier post, I'm fairly confident that the claim would hold. Earlier, I talked about the underlying assumptions of RVAs, comparing summation vs convolution in binding the context into a unique unit. The formalization for a given word vector is as follows: That is, the vector representing word i is the summation of all j context vectors in which i occurs. A context vector is defined as: In other words, a context vector is the convolution of the environmental vectors e, where each word has a uniquely associated environmental vector. (Here I use the product symbol for convenience – there isn’t an equivalent convolution symbol; interestingly, since I’m working with random vectors, the product works as effectively as convolution, since it yields a vector orthogonal to each compositional vector). Here, my goal is to expand my definition for a random vector accumulator by casting it as matrix algebra, rather than vector algebra. Let’s assume for each word, we have a one-hot, localist representation for each word, denoted as h. Instead of a set of environmental vectors e, we have a matrix E (with shape axb, where a is the length of h, here the number of words in the corpus, and b is the output dimensionality). We can then reformulate the construction of context vectors as Where is the localist representation for a word. Notably, yields a vector representation. This maintains consistency between this the earlier formulation formulation of context vectors. Instead of having a single vector that represents a word wi, we implement a word matrix W composed of all word vectors representing the words (W has the same shape as E). We can then define the matrix W as In other words, we sum all the one-hot vectors representing the words, and take the dot product with the transpose of the convolution of the words that occur in the same context, yielding a matrix representation of a given context. We then sum all such matrix representations together for all contexts in the corpus.
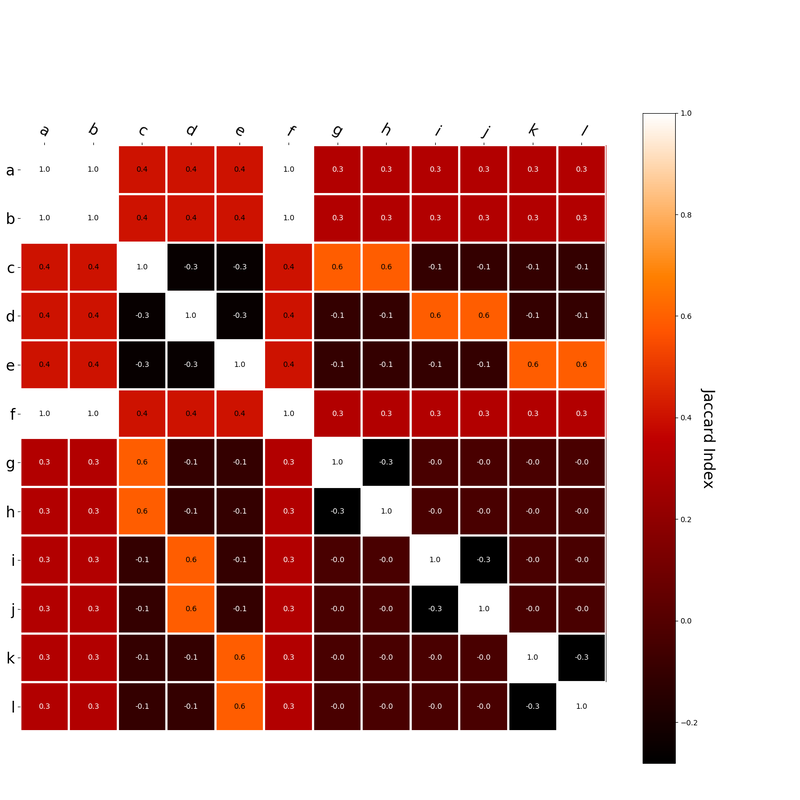
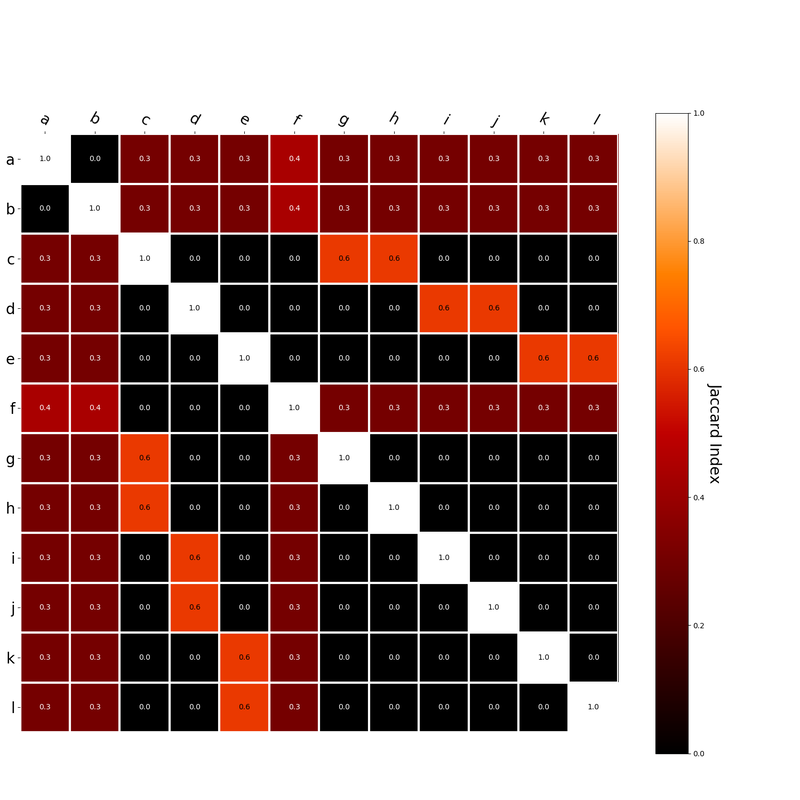
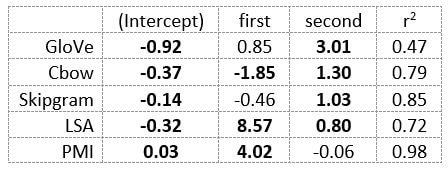
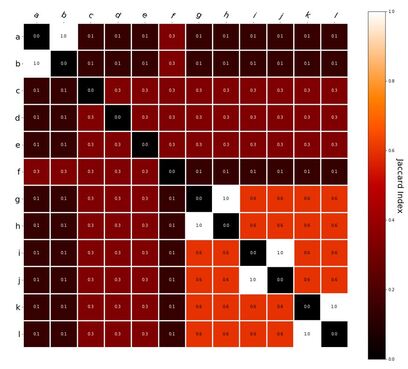
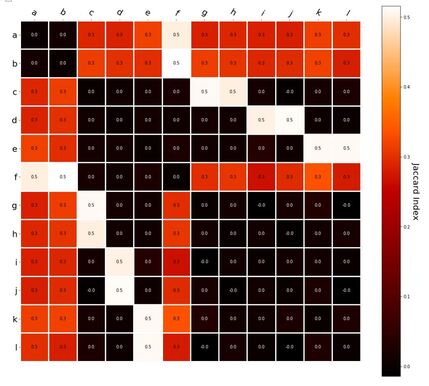
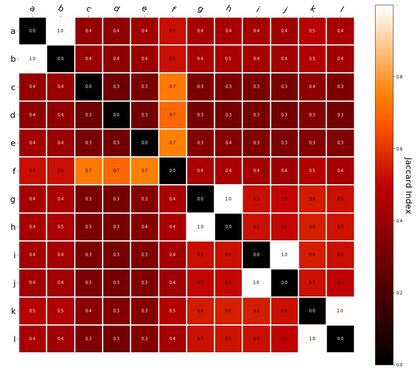
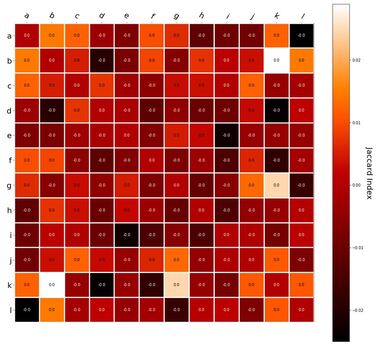
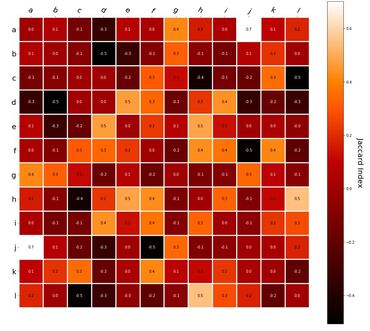
Since hk is a localist representation, this formulation is exactly equivalent to the earlier expression of an RVA. The usefulness of this expression is that instead of hk being a localist representation, we can instead define the vector representing a word as a distributed representation. Using a distributed representation yields a matrix W where columns no longer correspond to a given word, however this formulation yields the same predictions as a localist representation. We have, then, generalized RVAs to be effectively expressed as either localist or distributed networks. (The formalizations here might not be exactly right. I’m treating this more like a notebook than a submission for publication. At any rate, I’ve included code here where I step-by-step convert the word vector formulation to a matrix formulation.) I had this thought that cosine similarity judgments produced by distributional semantics models might be described as linear combinations of first and second order information. After all, the two main types of similarity identified in the literature are in regard to first order information (syntagmatic, thematic, related, contiguous) and second order information (paradigmatic, taxonomic, sometimes called just ‘similarity’). For an artificial corpus, I measured the first and second order associations between words. I then trained GloVe, cbow, skipgram, LSA, and PMI using the artificial grammar. I used the upper matrix (not including the diagonal) for the first and second order measurements in a linear model to predict the similarities produced by the DSMs via regression, where a DSM similarity is predicted as a weighted linear combination of first and second order information. I used python to train the DSMs and to produce the similarity matrices, I used R to produce the linear models predicting each DSM similarity matrix. I like heatmaps, so I’m going to include ALL OF THEM: The following table presents the coefficients for each linear model, where the coefficient is in bold if p<0.001. The variance accounted for by the model is included. (is there a better way to insert tables into weebly than taking a screenshot?) The interplay of significance and coefficient magnitudes tell an interesting story. PMI is clearly a measure of first order information. First and second order both significantly contribute to LSA, however first order information dominates. Word2Vec models are dominated by second order information (where first order information is suppressed). Glove is dominated by second order information (and it doesn’t seem like first order information is suppressed).
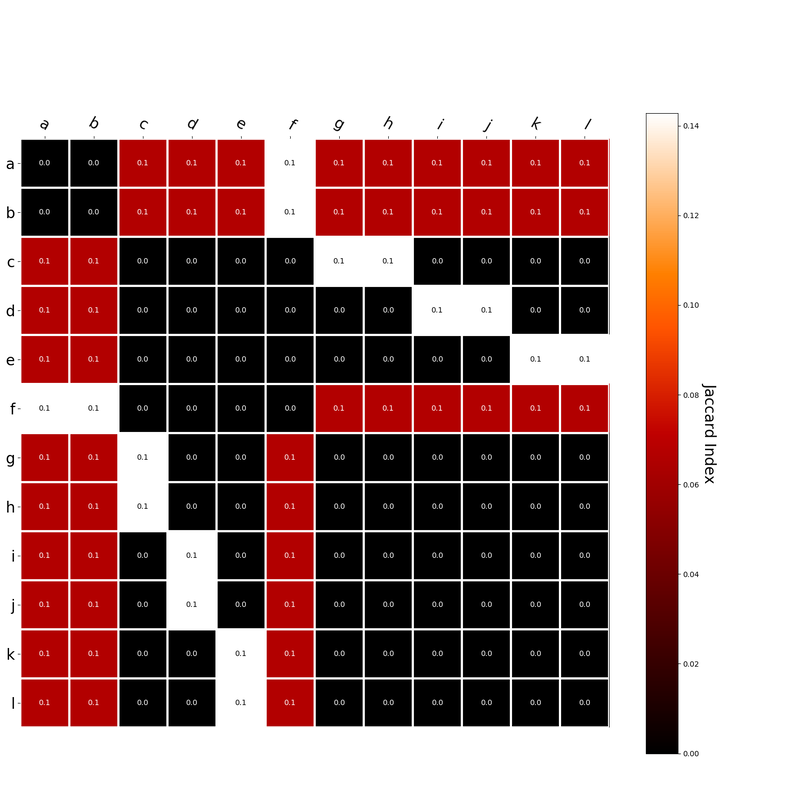
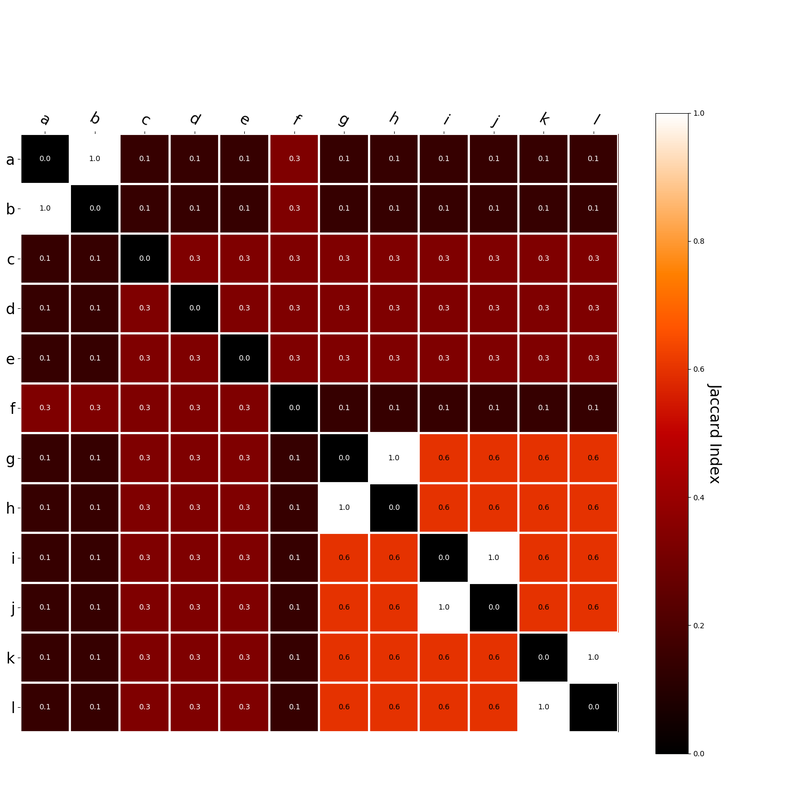
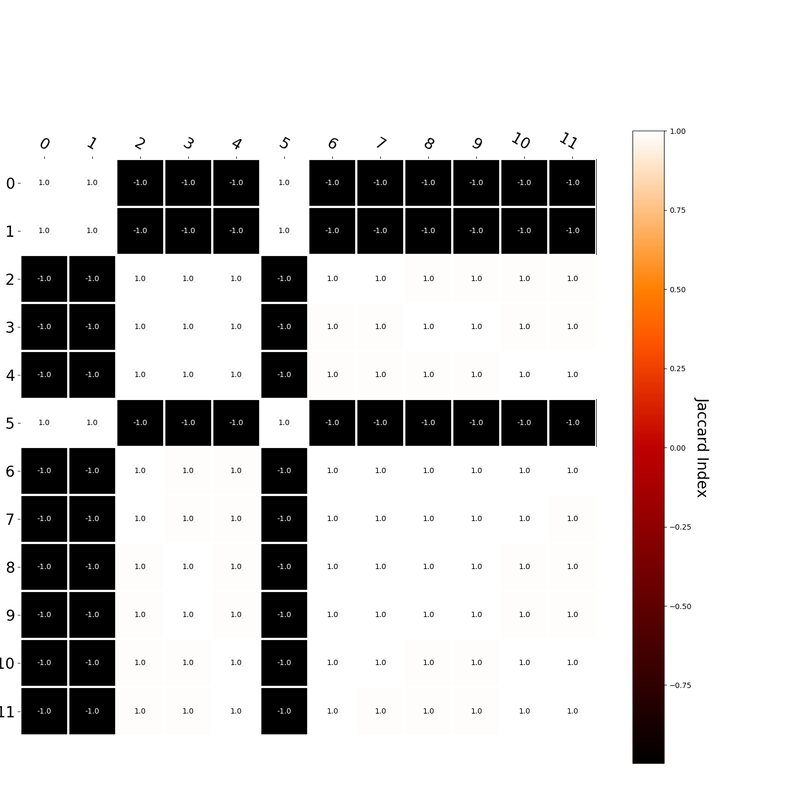
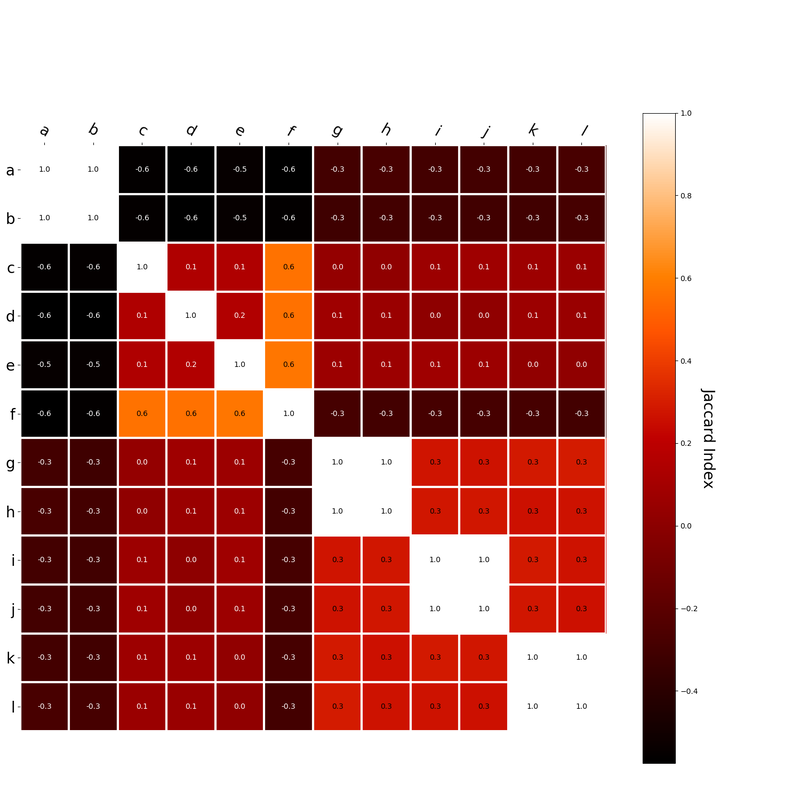
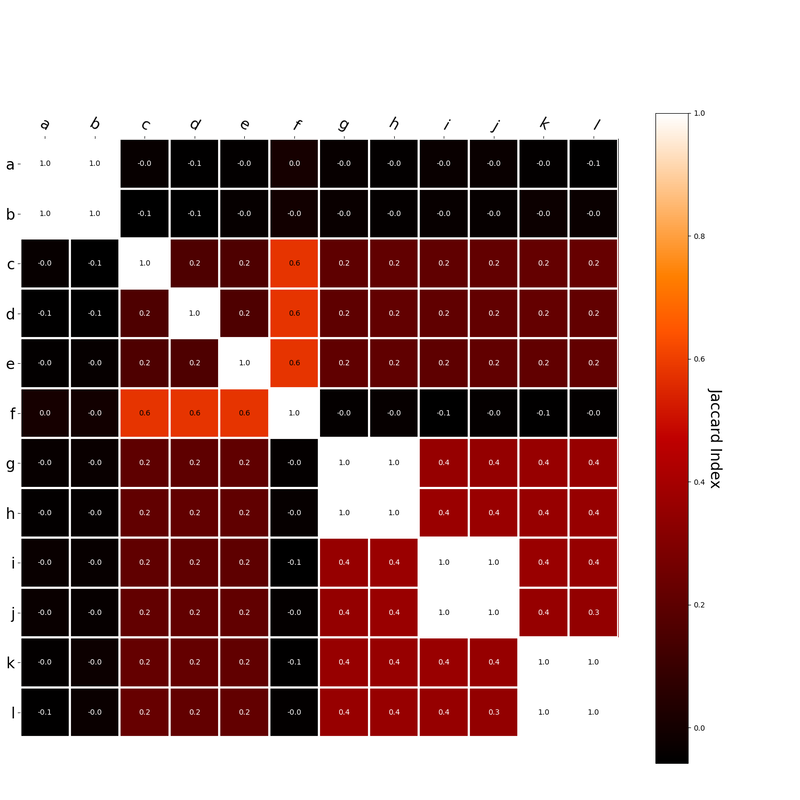
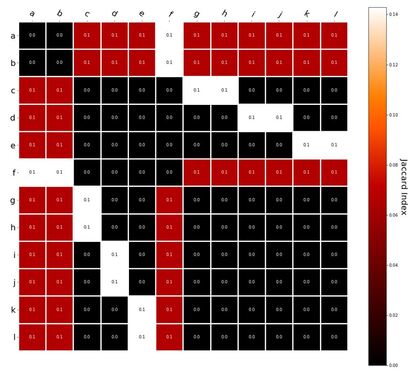
Interestingly, the variance subsumed by the linear model is the least for GloVe, at r^2=0.47. This suggests a few possibilities. It could indicate that GloVe is doing something in addition to first or second order information that is qualitatively different from what is being measured with first and second order information. It could also indicate that my method of measuring first and second order information is subject to its own limitations, where a different measure would come up with a prediction more akin to the similarity matrix produced by GloVe. When gathering similarity judgments, researchers tend to make a design decision to gather similarities based on second order information (e.g. SimLex-999), or first order information (e.g. thematic relatedness production norms from Jouravlev & McRae, 2016). Is there consistency between my measures of first/second order information and these datasets (spoiler, there is, but I only did correlations, not regression models; also, I didn’t include DSM in analysis – would DSMs match what is predicted here (eg GloVe would do well at SimLex, while PMI would do well at thematic)? Stay tuned for the next exciting adventure!) RVA can be constructed in two ways Assume the representation for a word w is a summation of the contexts in which the words occurred: The construction of the context of a word could be the summation of the environment vectors representing the words that occurred in the context. For instance, Then the representation of the word is: Alternatively, rather than construing the context as a summation, the vectors composing the context vector could be convolved into a vector that uniquely represents the context By properties of convolution, c1 and c2 are orthogonal vectors (given that the environmental vectors are orthogonal). Therefore, convolutional bindings yield a different model from the summation of environmental vectors. I used measures of first and second order statistics to yield these baseline heatmaps for word similarities: Expected first order based on jaccard index: Expected second order based on jaccard index First order information using convolutional bindings: Second order information using convolutional bindings: First order information using summation: Second order information using summation: It appears that binding contexts into a unique and orthogonal vectors is necessary in order to adequately recreate first and second order information. Additionally, this highlights how effective mapping a localist representation to a random vector could be for data reduction. (Later tests could involve RVA capacity – I can’t find sources that directly address this. Maybe plate has this info). (Also, could I make an incremental learner where environmental vectors aren’t previously assigned, but weights update iteratively based on co-activation?) Code for these analyses are available at my github. I don't like the way performance of semantic models is reported. It's impossible to compare results between papers. The results are as much a function of corpus choice and pre-processing as they are of the algorithm itself.
I think in my reporting of any new or unique set of data, I should submit results from basic DSMs - GloVe, LSA, CBOW, skip-gram, BEAGLE. That would demonstrate the effect I'm presenting relative to all of the models when under the same constraints of corpus choice and pre-processing. I've been playing with github recently. I thought it could be useful in handling experiment manipulations. I made a master branch for an experiment, then I have branches for each of the experimental manipulations. So far it seems pretty effective. It's a web experiment, and so when I want to collect data in a particular manipulation, I do a 'git checkout manipulation' call, and all of the files are updated appropriately. It sends the data to the same database, so I have branch IDs associated with each experimental manipulation, stored in the same tables. Also, I modify the readme per branch to track what the particular manipulation is. I'm kinda proud of this as a functional implementation for managing experiment variation. I've been keeping notes on best practices in the github repo readme. Unfortunately, I can't make the repo public as I accidentally included login info in a php file (didn't follow the best practice of employing the .gitignore file correctly smh). As it is, I'll just post my notes here. Maybe at some point I'll copy the repo without the sensitive info as a demonstration. ## General Operations
Master branch serves as main feature hub. Branches serve as experimental variations. Experimental variations include: distributions Each branch must include a 1) branch ID, which is included in the branch readme, and included in index.html to be saved with user data. 2) a thorough description of the experimental condition variations in the given branch. The readme for each branch indicates parameters specific to that branch only. Central modifications to the readme exist only on master branch. ## Experiment branch parameters Branch ID: Number of Cities: Distribution: Training Repititions: Number of Blocks: Sentence recognition questions per block: Sentences per block: Statement Sampling: Other modifications: ## General notes on using github for experiment development ### version management of experiments with github - local versions on computer - hosted on remote server - need to manage multiple variations of experiment ### solution: use git branching for each version of experiment ### must: incorporate documentation for each branch indicating version have root where core functionality is maintained versions are variations of master ### cannot: merge branch to master - the point is to have each manipulation of experiment well defined as branch ### steps: - created root experiment git repo (from local, github desktop) - when creating git repo that requires server access, use .gitignore to prevent copying sensitive info (passwords) to github - identical file structures for local and server (exists outside individual repo) - updated support repos (have a js plugin repo sitting, now it's active part of system) - copied repos to server - 'git clone https...' - had to change the user so that I got the credit instead of Rob - 'git config --list' shows configuration for git repo - 'git config user.name 'my_username' - updates git username associated with repo mods - 'git config user.email '[email protected]' - updates git email address - necessary to link account - Temporarily saving github credentials in cache - 'git config credential.helper cache' - followed by pull/push command, username and password are saved in cache for default 900 seconds - 'git credential-cache exit' - manually clears cache, probably good practice prior to logout ### Useful Git commands - Create a branch - I use Github desktop to manage this steps - Switch between branches - git checkout [branch] - View all branches - git branch ### Best practices for using git to manage experimental variations - Use the '.gitignore' file - Do not upload files with usernames and passwords to github - Log any files or folders with server access information into the .gitignore file to prevent accidental data insecurity - Use the master branch for the main code. For experimental variations, create a new branch. - Each branch must work independently, and any data logged must be tagged according to the variation. - In this experiment, I used multiple tables to track data. I shouldn't have. Instead, it would probably be better to track all data from an experiment in the same SQL table. - This includes any variation for the expriment. Not every entry will fill every column, but it will lead to more concise organization in the long run. A friend of mine just got a dog, and he asked me for advice. I proceeded to send him a tome. I figure I may as well put the advice here. This is my dog. His name is Bojack. He's pretty cool I guess. (When I see people walking their dogs, I angrily think about how my dog is cuter than their dog) Here's the advice I gave my friend: Let's see, I got bojack when he was big, though still a bit puppish and not great at peeing outside. my first suggestion is to buy a shload of carpet cleaner second suggestion is to take her outside every thirty minutes. in a couple of weeks you could up it to every hour, then every two hours. That's mostly how I got bojack to be good about peeing outside. third suggestion is to kennel train. I have a pamphlet somewhere. give me a sec I can't find it. here's a rundown and you can look up more specific information elsewhere. Feed your dog in the kennel. don't shut the door, just put the food bowl in there and let her eat. When she's done, she's done. After a week or two of that, you can start training her to go into the kennel (idk how training goes with younger pups, it might be early to start training word commands). The eventual goal is that the dog goes to the kennel immediately/enthusiastically every time you give the command. Reward it EVERY TIME (none of this variable reward bullshit, the dog is going to be stuck in there for a few hours, the least you can do is give it a treat). Also, kennel your dog up every time you leave the house for at least a year. None of this free range shit. It's only after a year that your dog has well-established habits, and you can start leaving it in a room, and then EVENTUALLY free reign of the house Older dogs behave better than younger dogs. Tired dogs behave better than fresh dogs Think ahead about the sorts of things you want your dog to be able to do. The most important thing for me was for bojack to drop something when I told him to. The worst thing I could imagine would be my dog biting some kid and not letting go. Here's a youtube channel I watched for how-tos on this and other topics: https://www.youtube.com/channel/UCZzFRKsgVMhGTxffpzgTJlQ Dogs are highly social and will pay attention to you for cues on their behavior. That is to say, your actions strongly impact the behavior and general temperament of the dog. You are a skinner box. If the dog does something you don't want it to do, don't reinforce it. If it does something you want it to do, positively reinforce it IMMEDIATELY (within a couple seconds, if you wait longer, the association between reward and the behavior you're trying to reinforce gets weak). Likewise, if it does something bad and you punish it, punish immediately, and then give a command that the dog can obey that you can reward (I have bojack sit, stay, come). Rewarding positive behavior should happen six times as frequently as punishing negative behavior. Never hit your dog. I haven't really focused on teaching bojack tricks. If I'm training something new, it's usually functional. That's just my preference. (caveat, when I'm feeding him, I ask him where I should put the food, and he points at the bowl. That's kindof fun)
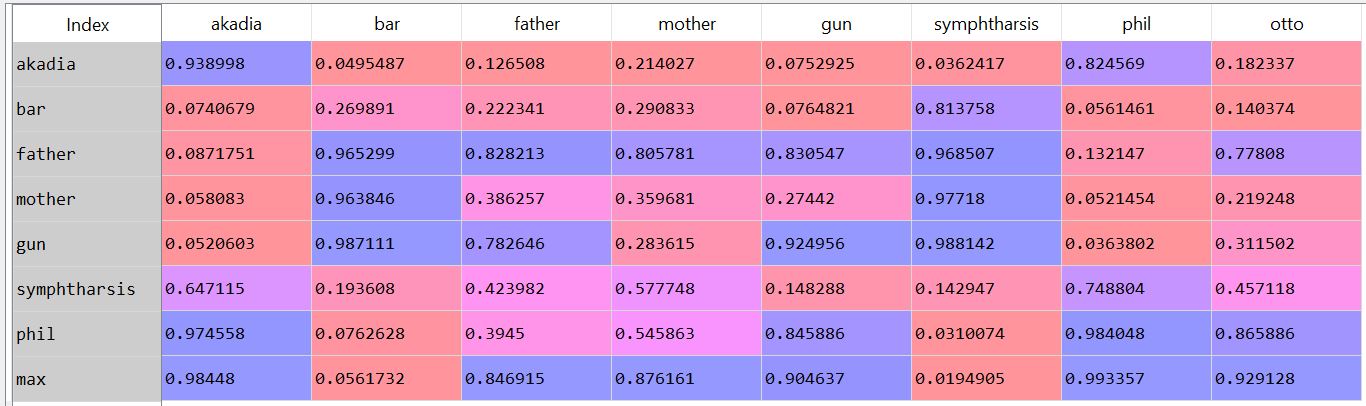
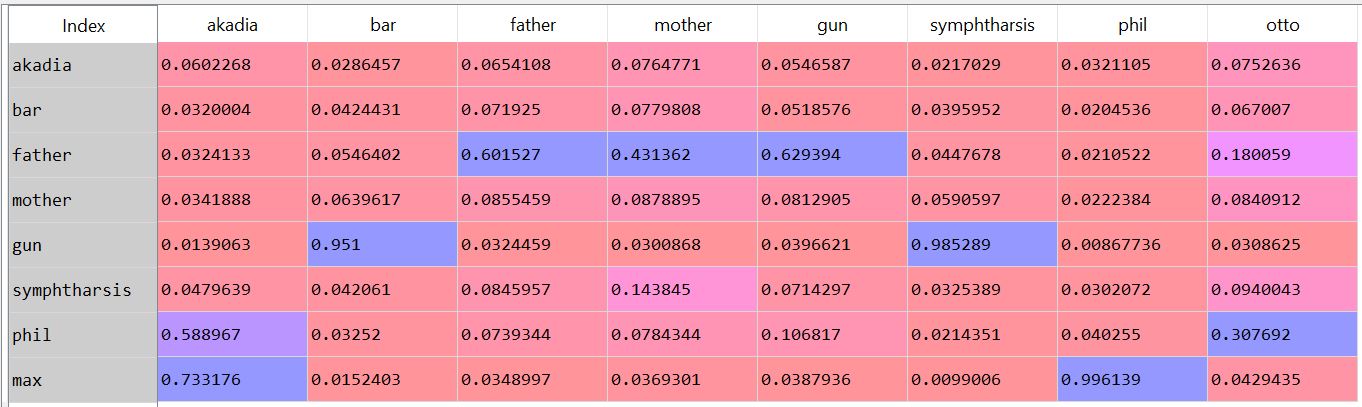
The things I think are important to teach my dog are, broadly, things to keep him alive (sit, stay, wait - since I don't have him on a leash nowadays, full disclosure, I had him for a year and a half before I even thought about doing that), and things to keep me from hating him (jumping at me, eating food that I didn't give him, sitting and waiting while I fill his bowl, etc). As you go through your new daily routine, think about how the dog is behaving and how your actions elicit different behaviors. Then choose the actions that elicit the behaviors from the dog that make you like the dog better. I tried out an approximated subgraph matching algorithm. I used Goldstone and Rogosky's (2002) algorithm called Absurdist. I applied it to text. I took the hausdorff index on a small set of words as a measure of their second order relationships within the text. I used my time travel story posted elsewhere. Since the two parts of the story mirrored each other, I thought it would be a good way to measure the degree to which the absurdist algorithm could map words onto one another. The results are interesting. 'Mother' and 'father' are confused for one another (not bidirectional, mother is confused for father in one direction, but not in the other). The characters max, phil, and akadia are confused for each other. Under some parameter settings, Otto matched with Max, which is neat (since the characters are mirrored). If I think of it later, maybe I'll post something more complete. As it is, a few notes. First, there's something weird about absurdist that doesn't scale. I had to modify the denominator of the value governing internal similarity (R in the model), such that it was treated almost like a probability distribution. Second, the output depends greatly on the preprocessing steps: window size (I tried a window of a word +- 3, 4, and 5), lemmatization/stemming (didn't do any of that), keeping stop words (kept it all in there), whether contexts spanned periods/line breaks (they did for me). Additionally, the parameters within the model play a large role. By changing chi and beta (the coefficients controlling inhibition and similarity, respectively), I can get varying results. For instance, here's when beta=.8 and chi = .2: And if I change inhibition to be greater (beta = .4, chi = .6): Same number of steps, but the low inhibition coefficient seems nicer (it's late, give me a break) (also, I would make nicer heatmaps rather than screenshots of the pandas dataframe, but again, it's late). The goal was to see whether absurdist would be able to adequately map the characters/words onto one another. It seems like we can (more or less) under particular conditions. Maybe I'll do some more work into making a robust pipeline. The code for this is on github. I use some functions in the code that I didn't include in the repository. Deal with it. The code for absurdist is there, so that might be useful. (I took a look at the java code that's posted online. It's in java, so it's too many hundreds of lines long. This sort of algorithm seems best implemented as matrix operations. As such, my implementation is ~50 lines long. Of course, I need to figure out why the thing isn't scaling, but I'm pretty sure the answer isn't in an extra thousand lines of code...) Cited: Goldstone, R. L., & Rogosky, B. J. (2002). Using relations within conceptual systems to translate across conceptual systems. Cognition, 84(3), 295-320. Most words have multiple senses.
I was looking at the occurrence of 'bee' in the TASA corpus. Of course, there's the insect, but then a couple of sentences popped up discussing spelling bees. Of course, this isn't a ground breaking observation. However, I could use the measure of second order relatedness I'm developing on the contexts that represent a single word. I could cluster the contexts together. Some (arbitrary?) threshold of cluster cohesiveness vs intercluster distance as definition for a given word sense. When comparing meanings between words, compare on the basis of the cluster of word senses that match, rather than also including the usages that don't relate to the word sense under scrutiny. |
AuthorIt's bad right now. It'll get better. Archives
March 2021
Categories
All
|
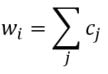
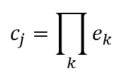
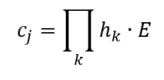
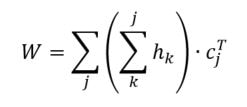
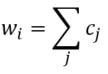
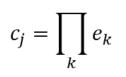
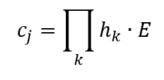
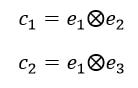





 RSS Feed
RSS Feed
