Extending first and second order characterization of DSMs

This is a continuation of an earlier analysis.

In summary, I used an artificial grammar to demonstrate that the cosine similarities predicted by a variety of DSMs could be well-characterized as linear combinations of direct measures of first and second order information.

I just had the idea that I could potentially use the linear model trained on the artificial grammar to predict similarities in natural language corpora. Using the same artificial grammar, I measured the first and second order information in the corpus​ (specifically, I used the jaccard index to measure the first order information, and a modification of the jaccard index to measure second order information; I should probably post about those measures sometime). I then trained a cbow model on the artificial corpus, and generated a cosine similarity matrix. I then trained a linear using scikit-learn to predict the cbow similarities using the measures of first and second order information.

THEN

I trained a cbow model on a natural language corpora. A small and easy one I have on hand is the tasa corpus (preprocessed, removing stop words, punctuation, but no lemmatization). I sampled a subset of 50 words randomly, and generated a cosine similarity matrix (I didn't do the entire corpus - there are 65,000 words - my computer can't handle a 65,000x65,000 matrix). I also measured the first and second order information for those same words in the TASA corpus.

FINALLY

I predicted the cbow similarities for the tasa corpus using the first and second order measures for the tasa corpus. AND!! It didn't work. The r^2 for the predicted data was well into the negatives. as it turns out, a linear model trained on a small amount of data doesn't extend well to naturalistic data. Who knew?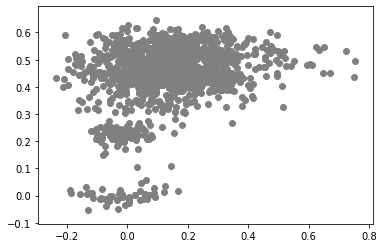

---

This boring looking plot is a scatter plot of the expected values against the predicted values. Along the x-axis are the cbow cosine similarities (expected), and the y-axis are the linear model predictions. While the plot looks promising, we don't get a significant prediction of the data. Wouldn't it be nice if we lived in a world where my simple prediction had been accurate? 


As it is, the regression produced by predicting cbow similarities in the artificial grammar do not generalize to predict the cbow similarities in the natural language corpus. Does this nullify my earlier claim that DSMs can be well-characterized as a linear combination of first and second order information? We'll see...

---

---

I performed the same analysis as in the demonstration using the artificial corpus. I generated a linear model predicting cbow cosine similarities using measures of first and second order information. Instead of performing the regressions in R or using scikit-learn, I used the statsmodels api (statsmodels gives me significance values, where I'd have to calculate them with scikit).

Linear Model - Artificial grammar:
cbow_sim = constant + first_order*b_0 + second_order*b_1
b_0 = -1.4***
b_1 = 1.06***
(magnitude and direction of coefficients indicates that cbow_sims are well-characterized by second order information)
r^2 = 0.78

Linear Model - Natural Language Corpus: 
cbow_sim = constant + first_order*b_0 + second_order*b_1
b_0 = 0.19
b_1 = 0.41***
(only coefficient for second order information is significant; not large, but still significant whereas the coefficient for first order information doesn't contribute significantly to the model)
r^2 = 0.11

The amount of variance predicted by the linear models significantly drops when I try to characterize cbow similarities in terms of first and second order information. First, I should note that the models DO still support my claim regarding first and second order information.

The drop in the variance predicted by the linear models may be due to multiple things. First, the measure of first and second order information might not be well suited for statements longer than three words (as three word statements are used in the artificial grammar). Second, I may not be training the cbow model adequately (or, the parameters of the cbow model aren't lined up to match the assumptions of the measures of first and second order information. ... I'm going to rerun something).

Is it likely that cbow is doing something qualitatively different in the natural language corpus from the artificial grammar? probably not. While I haven't put in the effort to test whether a linear model recreates the prediction of first vs second order information for every DSM I tested in my earlier post, I'm fairly confident that the claim would hold.