DSM similarities as linear combinations of first and second order information (also, I hate this font)

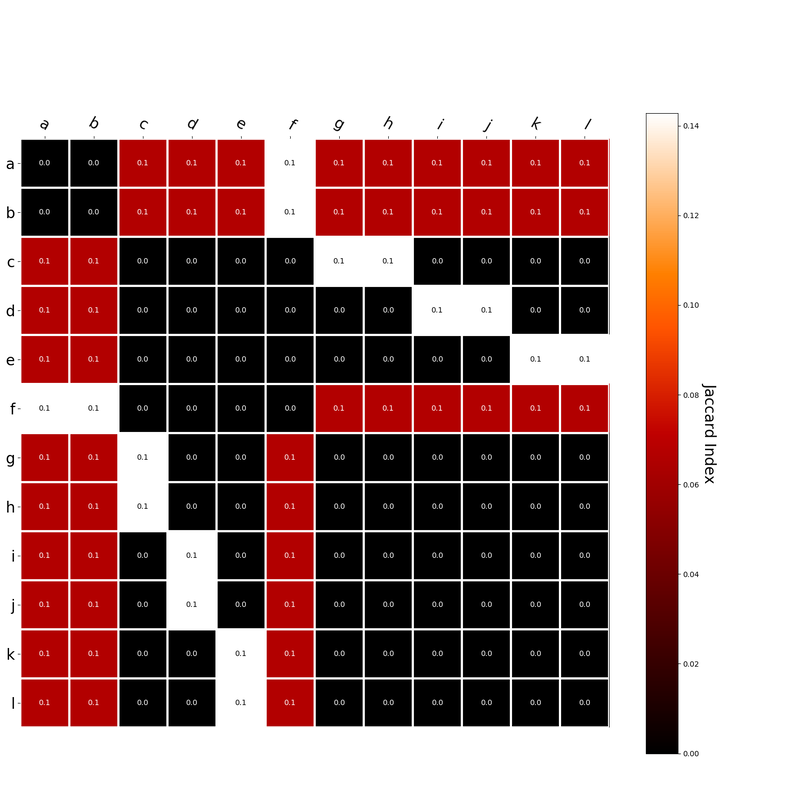
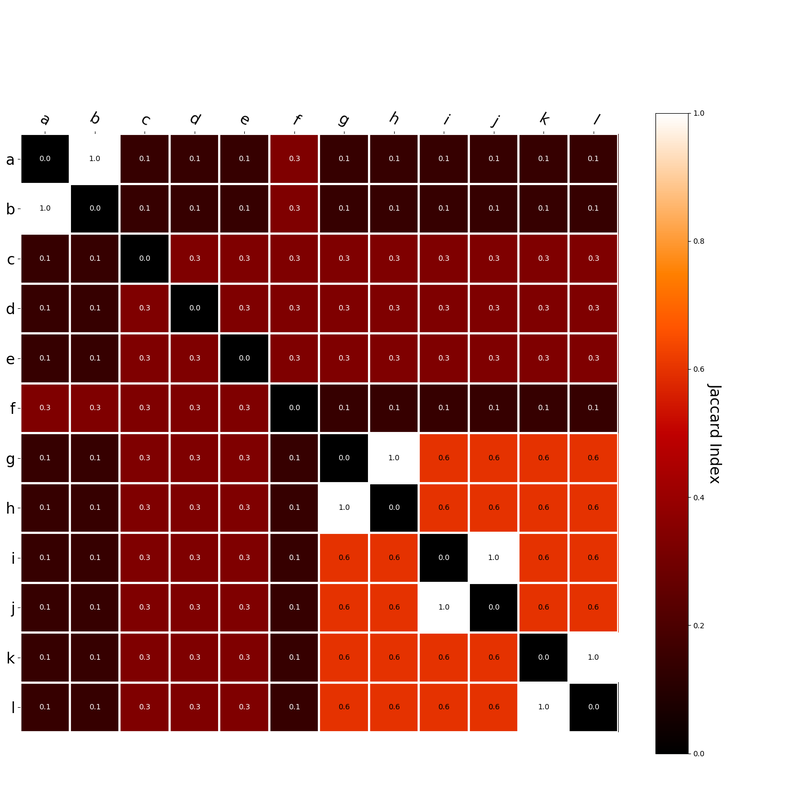
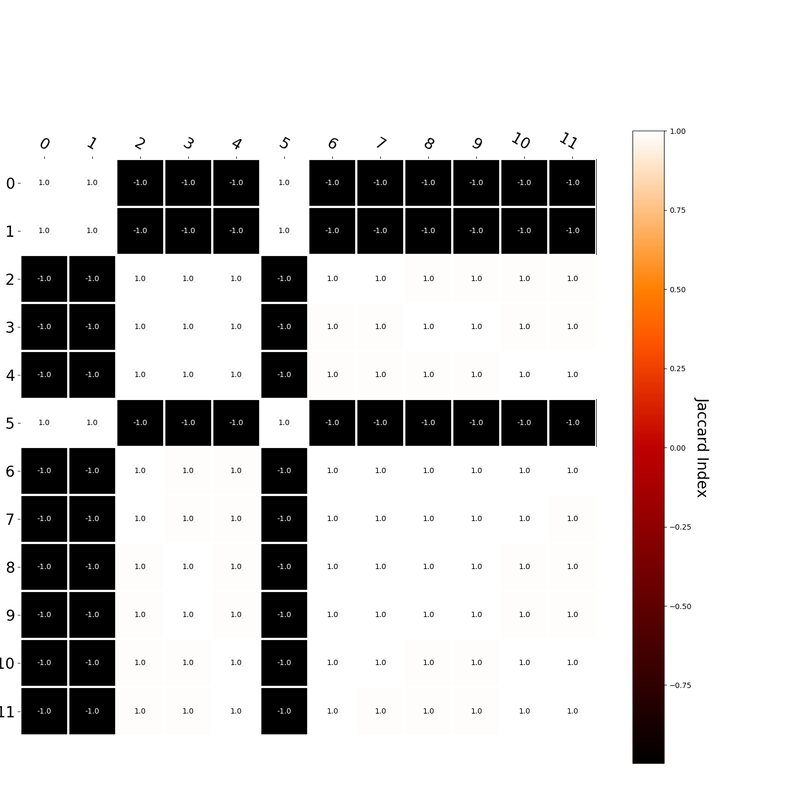
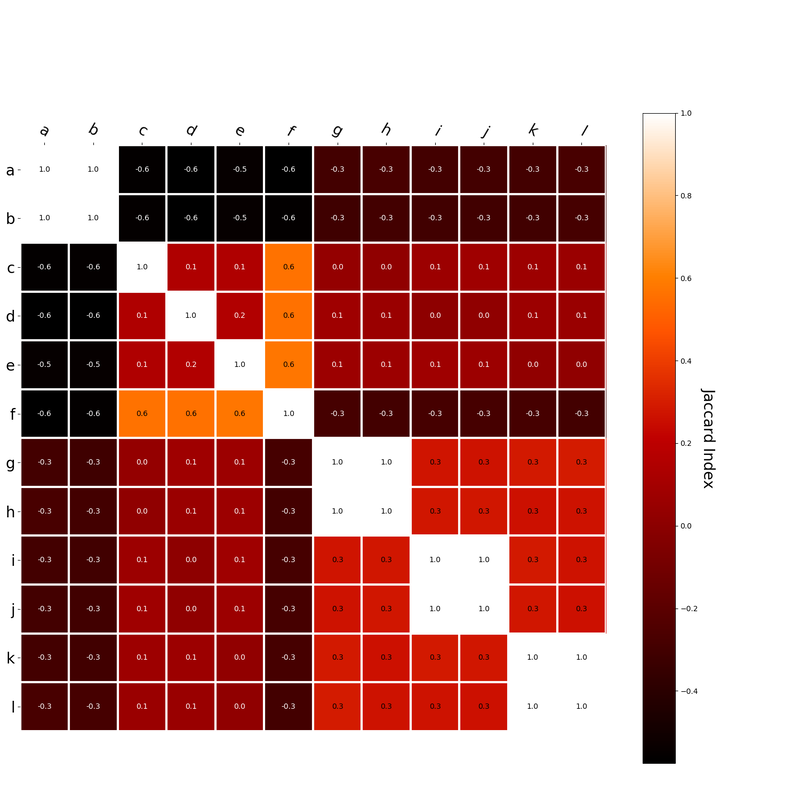
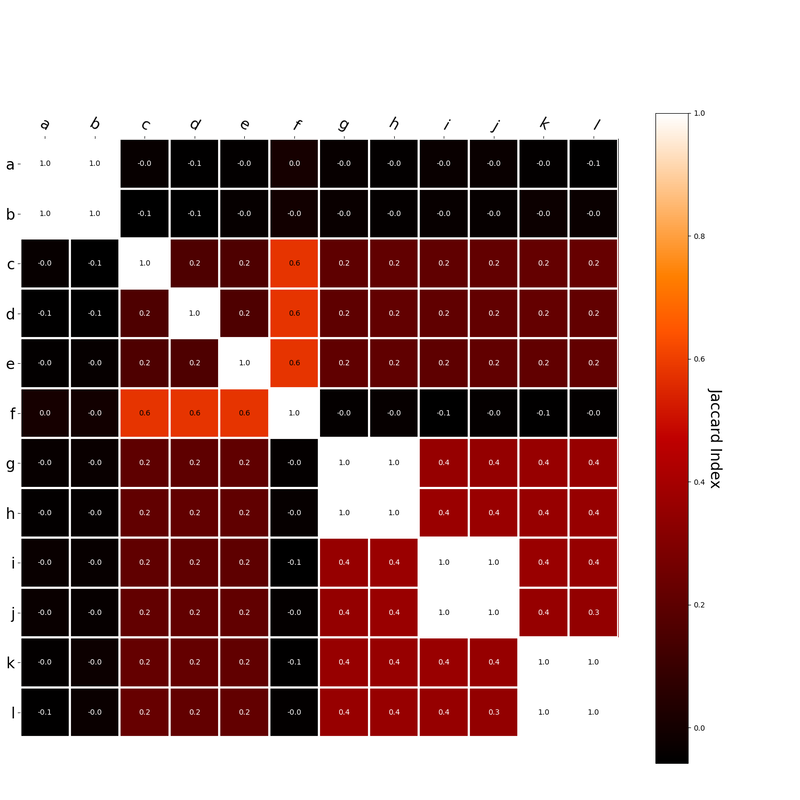
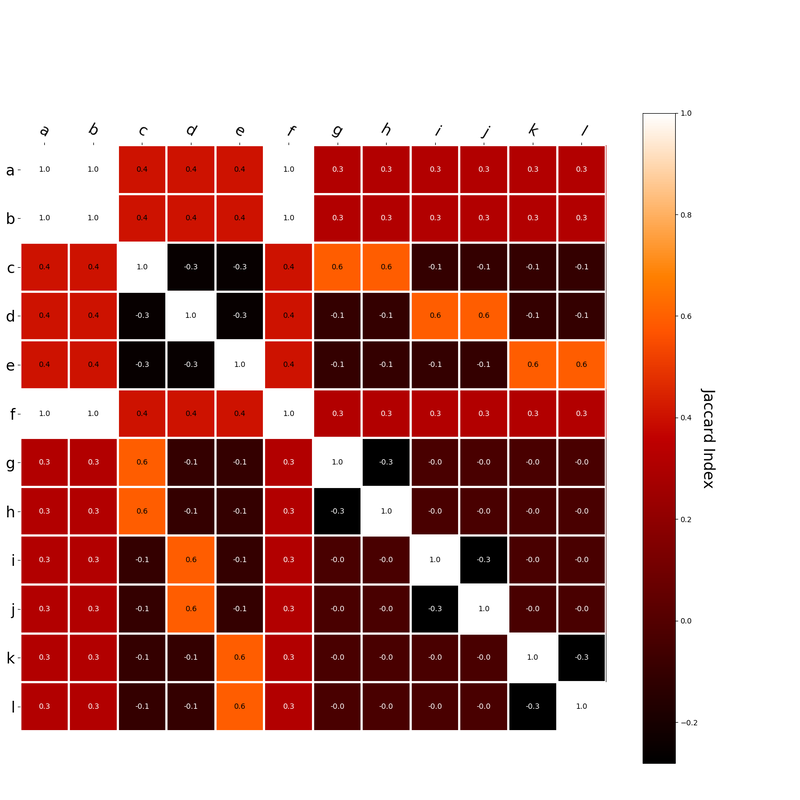
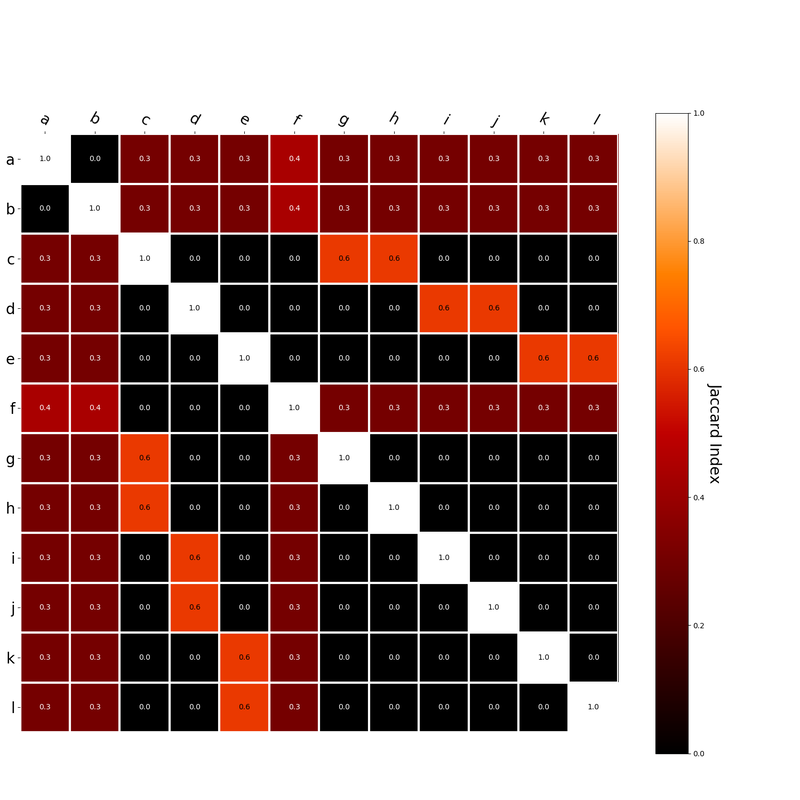
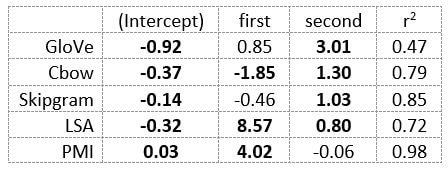
I had this thought that cosine similarity judgments produced by distributional semantics models might be described as linear combinations of first and second order information. After all, the two main types of similarity identified in the literature are in regard to first order information (syntagmatic, thematic, related, contiguous) and second order information (paradigmatic, taxonomic, sometimes called just ‘similarity’).

For an artificial corpus, I measured the first and second order associations between words. I then trained GloVe, cbow, skipgram, LSA, and PMI using the artificial grammar. I used the upper matrix (not including the diagonal) for the first and second order measurements in a linear model to predict the similarities produced by the DSMs via regression, where a DSM similarity is predicted as a weighted linear combination of first and second order information.  I used python to train the DSMs and to produce the similarity matrices, I used R to produce the linear models predicting each DSM similarity matrix.
​
I like heatmaps, so I’m going to include ALL OF THEM:

First order information

Second order information

GloVe

CBOW

Skip gram

LSA

PMI

​The following table presents the coefficients for each linear model, where the coefficient is in bold if p<0.001. The variance accounted for by the model is included. (is there a better way to insert tables into weebly than taking a screenshot?)

The interplay of significance and coefficient magnitudes tell an interesting story. PMI is clearly a measure of first order information. First and second order both significantly contribute to LSA, however first order information dominates. Word2Vec models are dominated by second order information (where first order information is suppressed). Glove is dominated by second order information (and it doesn’t seem like first order information is suppressed).

Interestingly, the variance subsumed by the linear model is the least for GloVe, at r^2=0.47. This suggests a few possibilities. It could indicate that GloVe is doing something in addition to first or second order information that is qualitatively different from what is being measured with first and second order information. It could also indicate that my method of measuring first and second order information is subject to its own limitations, where a different measure would come up with a prediction more akin to the similarity matrix produced by GloVe.
​
When gathering similarity judgments, researchers tend to make a design decision to gather similarities based on second order information (e.g. SimLex-999), or first order information (e.g. thematic relatedness production norms from Jouravlev & McRae, 2016). Is there consistency between my measures of first/second order information and these datasets (spoiler, there is, but I only did correlations, not regression models; also, I didn’t include DSM in analysis – would DSMs match what is predicted here (eg GloVe would do well at SimLex, while PMI would do well at thematic)? Stay tuned for the next exciting adventure!)

Code for these analyses are available at my github.