|
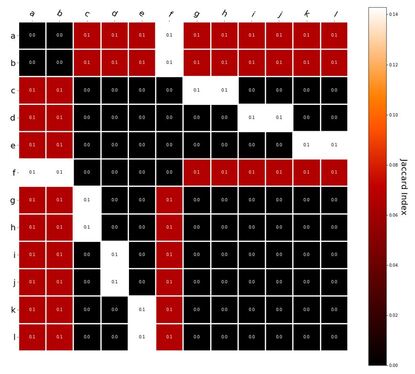
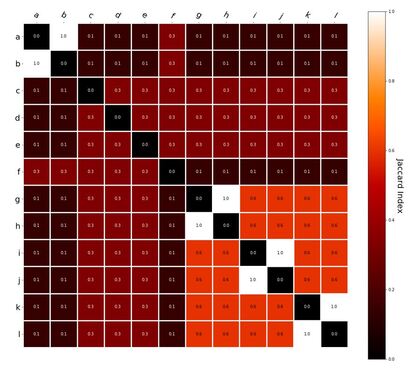
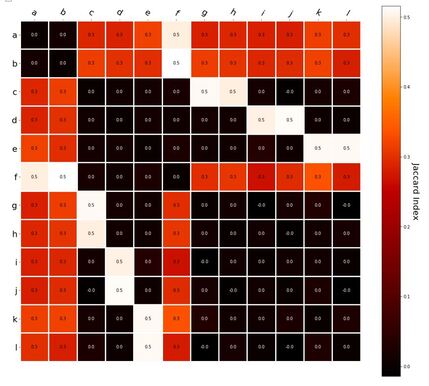
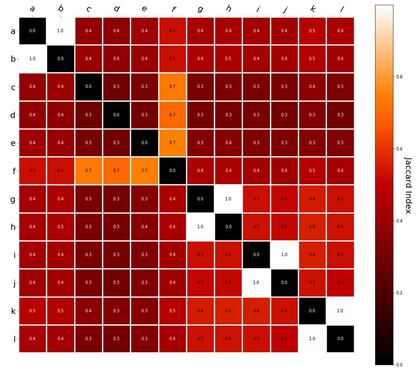
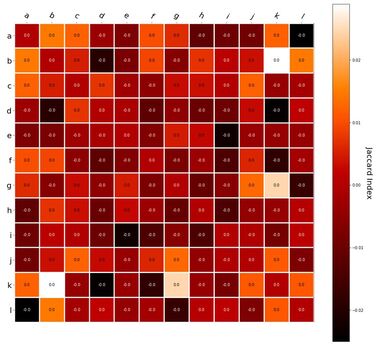
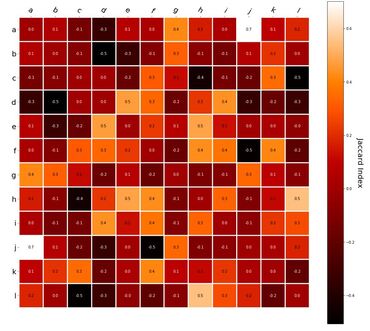
RVA can be constructed in two ways Assume the representation for a word w is a summation of the contexts in which the words occurred: The construction of the context of a word could be the summation of the environment vectors representing the words that occurred in the context. For instance, Then the representation of the word is: Alternatively, rather than construing the context as a summation, the vectors composing the context vector could be convolved into a vector that uniquely represents the context By properties of convolution, c1 and c2 are orthogonal vectors (given that the environmental vectors are orthogonal). Therefore, convolutional bindings yield a different model from the summation of environmental vectors. I used measures of first and second order statistics to yield these baseline heatmaps for word similarities: Expected first order based on jaccard index: Expected second order based on jaccard index First order information using convolutional bindings: Second order information using convolutional bindings: First order information using summation: Second order information using summation: It appears that binding contexts into a unique and orthogonal vectors is necessary in order to adequately recreate first and second order information. Additionally, this highlights how effective mapping a localist representation to a random vector could be for data reduction. (Later tests could involve RVA capacity – I can’t find sources that directly address this. Maybe plate has this info). (Also, could I make an incremental learner where environmental vectors aren’t previously assigned, but weights update iteratively based on co-activation?) Code for these analyses are available at my github.
0 Comments
Your comment will be posted after it is approved.
Leave a Reply. |
AuthorIt's bad right now. It'll get better. Archives
March 2021
Categories
All
|
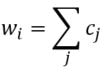
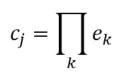
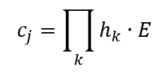
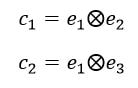
 RSS Feed
RSS Feed
