Instead of Cosines

A common theme my advisor brings up is the idea that cosine similarity is not what humans do.

I want to break that down a bit and consider what that means with regard to the representation of modalities in semantic vectors.

The typical way to make use of text-derived semantic vectors is to evaluate the similarity between words (aka the cosine similarity) and compare the similarities produced by the model against similarities produced by human judgments. With this approach, the extent of the usefulness of semantic vectors is something like a k-nearest-neighbors application. Of course, knn is useful for categorization. However, knn can't be the entirety of the usefulness of semantic vectors (an ideological stance that I will pursue until I find evidence ... like a good scientist).

Instead of the extent of the usefulness of semantic vectors being in knn, we can treat the distribution of points in high dimensional space as meaningful and useful as is. And just as with (nonmetric) multidimensional scaling, which is rotation and scale invariant (among other things), the exact location of a word in high dimensional semantic space isn't inherently meaningful. It's the position of a word relative to another word. Likewise, MDS is often applied such that the dimensions become interpretable in some way. In a high dimensional semantic space, the dimensions likewise aren't inherently meaningful, but it seems likely that I ought to be able to rotate the semantic space in order to yield meaningful dimensions.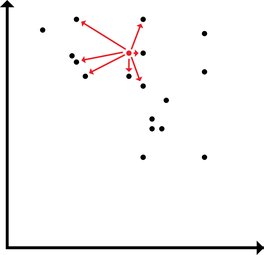

---

Typically, the usefulness of a vector in semantic space is applied by comparing discrete positions of a given word to the positions of other surrounding words (or of words that we would expect a model to produce a given similarity rating for).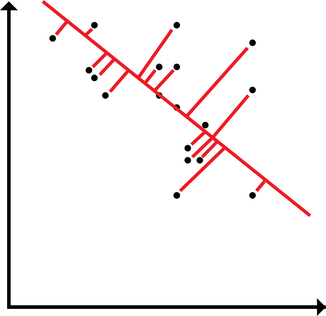

---

---

However, words may be distributed in space along some arbitrary high dimension latent within the structure that maximizes the relationship between a word in high dimensional space and some external behavior. Here, I demonstrate how words could load onto a latent dimension, where the latent dimension could predict, say, modality ratings yielded by participants. The way a word may load onto a particular modality may be latent and unobservable directly in the nearness between words in the semantic space, but may be retrievable.

---

---

A simple way to implement this would be linear regression. Using sensorimotor norms as a target to predict, we could draw a line through the high dimensional space and see how each word loads onto the line.

Alternatively, we could render interpretable dimensions by constructing a rotation and shift matrix. By rotating and shifting the matrix, a given dimension could be used to predict something like sensorimotor norms. Additionally, the space could be rotated to maximize each of the modalities in the norms (and then, following from the GCM, decisions could be made by applying different attentional weights to a different dimensions depending on the task.

I tend to like the second approach better, but regression is easier to implement off the top of my head. Stay tuned to see whether I actually try this out! :D

---

Note to self: I could do something like multi-fold testing in data mining using a rotation matrix yielded by procrustes analysis. I could build the rotation matrix using some subset of the data, then test the rotation matrix using the other partition. I rather prefer this to linear regression (I suppose, it's a multi-constraint linear regression): it preserves the space, and it can be interpreted in terms of a neural network.