|
Earlier, I talked about the underlying assumptions of RVAs, comparing summation vs convolution in binding the context into a unique unit. The formalization for a given word vector is as follows: That is, the vector representing word i is the summation of all j context vectors in which i occurs. A context vector is defined as: In other words, a context vector is the convolution of the environmental vectors e, where each word has a uniquely associated environmental vector. (Here I use the product symbol for convenience – there isn’t an equivalent convolution symbol; interestingly, since I’m working with random vectors, the product works as effectively as convolution, since it yields a vector orthogonal to each compositional vector). Here, my goal is to expand my definition for a random vector accumulator by casting it as matrix algebra, rather than vector algebra. Let’s assume for each word, we have a one-hot, localist representation for each word, denoted as h. Instead of a set of environmental vectors e, we have a matrix E (with shape axb, where a is the length of h, here the number of words in the corpus, and b is the output dimensionality). We can then reformulate the construction of context vectors as Where is the localist representation for a word. Notably, yields a vector representation. This maintains consistency between this the earlier formulation formulation of context vectors. Instead of having a single vector that represents a word wi, we implement a word matrix W composed of all word vectors representing the words (W has the same shape as E). We can then define the matrix W as In other words, we sum all the one-hot vectors representing the words, and take the dot product with the transpose of the convolution of the words that occur in the same context, yielding a matrix representation of a given context. We then sum all such matrix representations together for all contexts in the corpus.
Since hk is a localist representation, this formulation is exactly equivalent to the earlier expression of an RVA. The usefulness of this expression is that instead of hk being a localist representation, we can instead define the vector representing a word as a distributed representation. Using a distributed representation yields a matrix W where columns no longer correspond to a given word, however this formulation yields the same predictions as a localist representation. We have, then, generalized RVAs to be effectively expressed as either localist or distributed networks. (The formalizations here might not be exactly right. I’m treating this more like a notebook than a submission for publication. At any rate, I’ve included code here where I step-by-step convert the word vector formulation to a matrix formulation.)
0 Comments
Your comment will be posted after it is approved.
Leave a Reply. |
AuthorIt's bad right now. It'll get better. Archives
March 2021
Categories
All
|
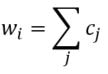

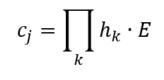
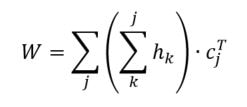
 RSS Feed
RSS Feed
