Random vector accumulators

I recently wrote some code for a random vector accumulator. It worked pretty fast. But the reason it worked fast was because it was just a matrix multiplication between a word-by-word matrix and a matrix of random vectors. Upon reflection, I came to the frustrating conclusion:

A random vector accumulator doesn't do anything that a word-by-word co-occurrence matrix doesn't do.

Specifically: if the random vectors are defined as having a length of one, and a cosine similarity of zero with any other vector, then a sparse vector where only one element is one and the rest of the elements are zero fulfills this requirement. In this way, a count matrix can be construed as a special case of the random vector accumulator.

Additionally, the random vectors add no information in addition to a word-by-word count matrix. Below are two MDS renderings of a given word list. First is the rendering for the RVA, the second is the rendering for the WxW matrix. The bidimensional regression yields an r value of 0.996, quantitatively demonstrating that the two renderings are a near-perfect match (only near-perfect because of the small amount of noise from the random vectors).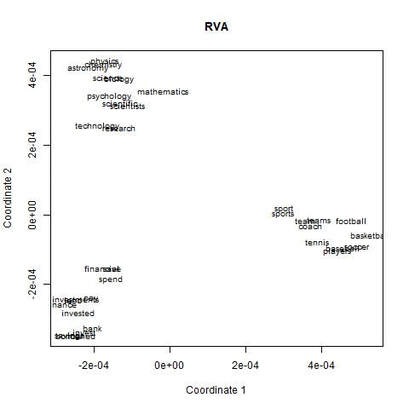

MDS projection of a selection of words (used in Jones & Mewhort, 2007). The words are drawn from three clusters in order to demonstrate the model's ability to correctly group similar words. The random vectors have 1000 elements/dimensions.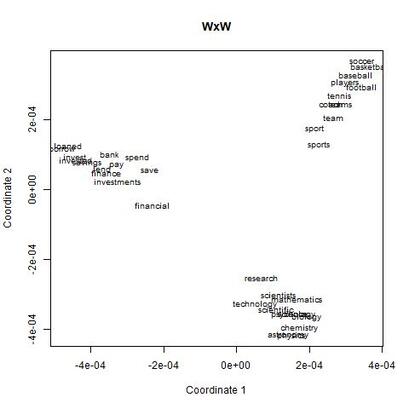

---

The word by word matrix is a raw frequency count of words that co-occur in the same context. Context is arbitrarily defined - here it's the co-occurrence of words within a paragraph.

---

Upon further reflection (after it was pointed out to me), I realized that the nearly perfect reproduction of the WxW matrix by the RVA is a feature rather than a bug. While the RVA doesn't serve to reveal any latent relationships between words, it effectively compresses the matrices. The WxW matrix is ~95,000x95,000. The RVA matrix is ~95,000x1000, effectively (and with high accuracy) reducing the matrix to one one-hundredth of the size. 

(In practice, I used a scipy.sparse.csr_matrix to implement the count matrix - storing a 95,000x95,000 matrix in my computer's memory would be a mission; additionally, the transformation from a WxW matrix to an RVA is a simple matrix multiply between two matrices. The computation is sped up if I only use the words of interest from the WxW document. In this example, it was a matrix multiplication of my W'xW matrix [35,95000] and my random vectors [95000,1000] - which is a pretty quick computation. I've posted the code here.)

In order to satiate my interest in RVAs, I looked at the ability of an RVA to reproduce the distributions of a random set of 1000 words at varying dimensionalities.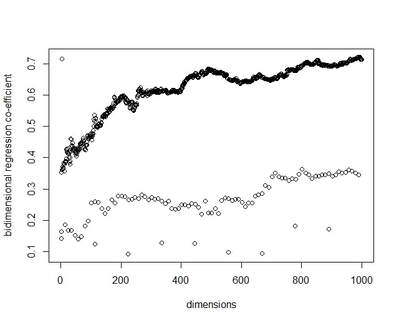 

The x-axis is the varying number of dimensions. The y-axis is the bidimensional regression co-efficient (Friedman & Kohler, 2003; bidimensional regression is a measure of how well two plots match each other, independent of flips or rotations)

---

Note that the RVA performance peaks at 0.7 rather than 1 (as in the above example). This is due to an interaction of the word set and the bidimensional regression measure. Plots that are well-clustered are generally easier to reproduce. Since I chose random points, any reproduction of the plot is going to be much noisier (I don't have a mathematical explanation for this, it's based on intuition earned from another project regarding spatial layouts; potentially forthcoming as a blog post).

There are a couple interesting points to note about this plot. First, there is a roughly linear increase in performance with dimensionality. This is to be expected. But there's this weird harmonic looking thing happening, where at certain intervals, the model drops in performance. I don't have any explanation for this (but I ran it multiple times to the same effect). It's neat, but weird.

In final consideration, using a sparse matrix may still be more efficient. With a sparse matrix, I may have to store fewer actual elements than if I store a random vector. Potentially, instead of a random vector, there could be optimal vectors that I could use to reduce dimensionality while also reducing the actual number of elements that have to be stored.