|
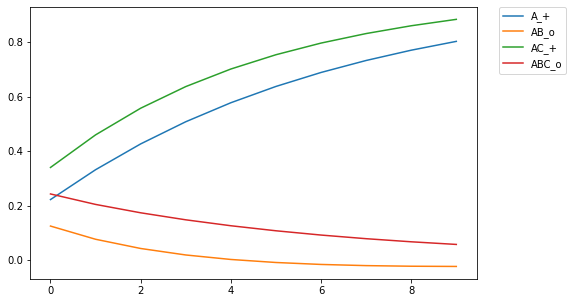
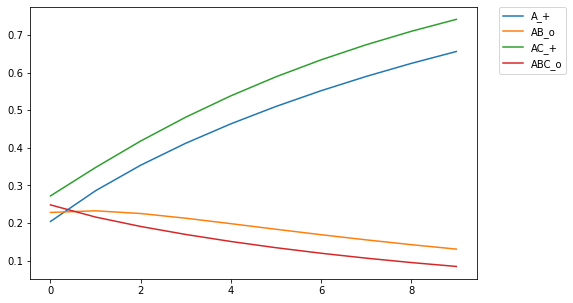
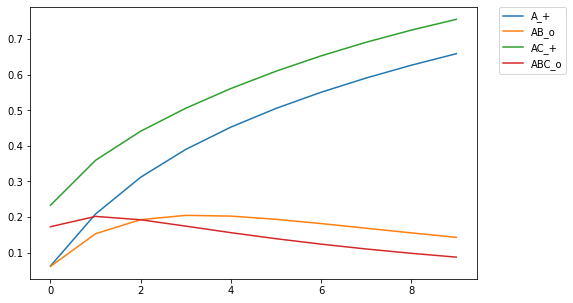
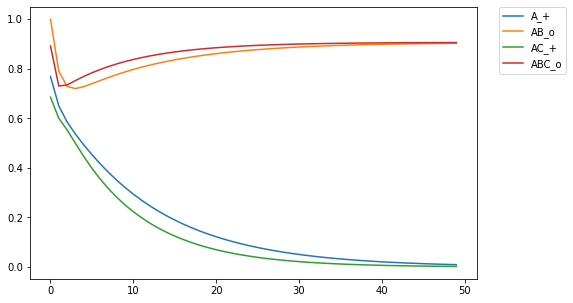
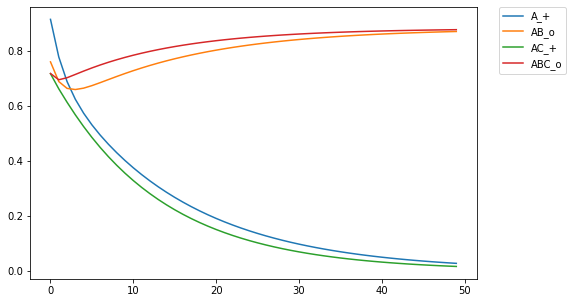
My numerous readers have been waiting with bated breath, but they must suffer this long wait no longer. For behold, I have generalized the rescorla-wagner learning model (Rescorla & Wagner, 1972) into a format that is generally interpretable in linear algebra. It turns out that psychologists are kinda bad at math, and there was some translation issues that I needed to work through to make sure everything worked the way it was supposed to. Originally, the RW update rule was as followed (equations copied from wikipedia): and Where V_x is the association strength between a cue and a response. Alpha and beta are learning parameters (beta is a global parameter while alpha is a cue parameter). V_tot is the current activation of the response given the cue. Lambda is the expected response given a cue. As it currently stands, this notation is only good for associating a single response with a limited set of cues. The point is it's not very effective notation, so I'm going to generalize the notation to be interpretable, using modern day conventions in discussing networks. Changes in notation: Lambda -> r, where r is a row vector of real numbers, size m. c is the expected output of the model c, where c is a row vector of real numbers, size n. c is the input field of the model. V -> W, where W is a weight matrix with nxm dimensions, where n is the number of input nodes, and m is the number of response nodes alpha and beta are scalar learning parameters, and can be left as such V_tot -> never explicitly defined *anywhere*. = c @ V, where @ indicates the dot product. Using this definition, the weight matrix update rule for any cue/response, input/output pairing would be: I tested this using the examples in my previous blog post. First, when training a single discriminator on all c-r pairings: Then using 2 discriminators: I then projected the cue field into a space with 50 dimensions. By sampling from a gaussian distribution, I generated orthogonal vectors for each of the input cues (Plate, 2003). I then got a simple linear projection of the cue field into a high dimensional space by taking the dot product between the cue field and the projection matrix. Since 50 dimensions is low, the results tend to be noisy, but get the same qualitative effect: I then projected the response field into 50 dimensions, returning the cue field to the original localist representation (if you want to make sure something works, you gotta do it in baby steps. Baby steps to the door. Baby steps down the stairs. Baby steps to a generalized implementation of the rescorla-wagner learning rule). After training the network, I found the euclidean distance from the the network output to the projection matrix. When the network produced the correct output, there was a smaller distance from the response field to the projection matrix, which yields an inverted graph (note, the colors are consistent between all plots): Finally, I tried the learning rule with projecting both the cue and response fields into a higher dimensionality. (I should find a lesson on how to work with arrays with high number of axes. I know that at this point everyone's mother plays with tensors like a toddler (me) plays with playdough. But I need a hand ugghhh). Anyway, it works and looks lovely! Future directions. I need to do the other examples that Pearce (1994) describes. I think his configural cue theory can easily be handled in a high dimensional space using convolution (where a configuration of a and b is the convolution of two vectors representing a and b, since convolution yields an orthogonal vector). This would allow there to be an arbitrary number of configurations without the need for increasing the number of nodes in the model (i.e. no need for a third node representing the configuration of a and b). Also, out of idle curiosity, I wonder if I can train a multi-layer network using this update rule. how would that work? how would I update each layer of the network? Is it possible? With R-W there's still an objective function. But I'm thinking of something like a kohonen map, is there a way for the firings of input nodes to self organize so that they 'sort out' different types of inputs? Could be easy with orthogonal inputs - I would just want some number of output nodes to align with a given input. idk. it's just a thought. The goal is something that is a locally-derived update function, rather than a globally derived objective function. That just seems more interesting to me than like a backpropogation algorithm (if networks) or a linear algebra solution like LSA or GloVe. The code for this post is here. I don't think my previous blog post had its associated code, which I'll place here. Anyway, I've satisfactorily avoided my work so far today. I'd actually better get to it. Best, with love, yours truly, etc. References:
Pearce, J. M. (1994). Similarity and discrimination: A selective review and a connectionist model. Psychological Review, 101(4), 587. Plate, T. A. (2003). Holographic Reduced Representation: Distributed Representation for Cognitive Structures. CSLI Publications. https://books.google.com/books?id=cKaFQgAACAAJ Rescorla, R. A., & Wagner, A. R. (1972). A theory of Pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement. Current Research and Theory, 64–99.
0 Comments
Your comment will be posted after it is approved.
Leave a Reply. |
AuthorIt's bad right now. It'll get better. Archives
March 2021
Categories
All
|
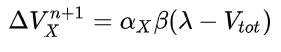
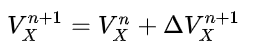
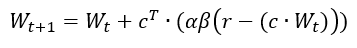
 RSS Feed
RSS Feed
